5.1 Monte Carlo Prediction

value function : expected return (cumulative future reward) starting from that state.

The idea underlies MC methods is to estimate a value function by experience by averaging the returns observed after visits to that state.

Suppose we wish to estimate $v_{\pi}(s)$, the value of a state $s$ under policy $\pi$.

• visit is an occurrence of state $s$ in an episode
• $s$ may be visited multiple times in the same episode
  • first visit to $s$ is the first time it is visited in an episode
• The first-vist MC method
  • it estimates $v_{\pi}$ as the average of the returns following first visits to $s$
• The every-visit MC method
  • is the average of the returns following all visits to $s$
• Both methods converge to $v_{\pi}$ as the number of visits (or first visits) to $s$ goes to infinity

For DP methods, you must have complete knowledge of the environment and sometime it is hard to find some quantities needed for computation (like $p(s',r|s,a)$). In some game (like black jack for example), it is really hard to determine those quantities. MC methods does not have this issue because we are working with sample. Generating the sample you will work with is often easier than to determine the one needed for DP.

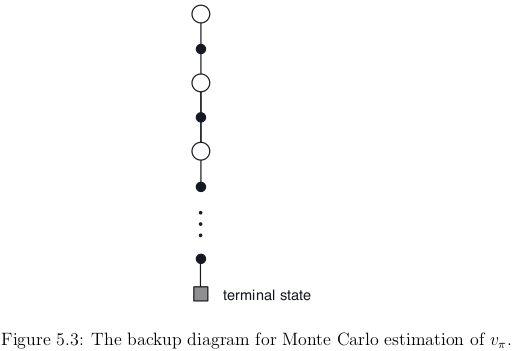
Backup diagrams are pertinent and we can generalize the idea to MC algorithms.

• backup diagram idea is
  • to show at the top the root node to be updated
  • to show below all the transitions and leaf nodes whose rewards and estimated values contribute to the update

• In MC estimation of $v_{\pi}$

  • the root is a state node
  • below is the entire trajectory of transitions along a particular single episode
    • ending at the terminal state

• Difference between DP diagram (Figure 3.4) and MC diagram (Figure 5.3)

  • DP diagram shows all possible transitions
  • DP diagram shows only one-step transitions
  • MC diagram shows only those sampled on the one episode
  • MC diagram goes all the way to the end of the episode

• each estimation for each state are independent in MC methods
• MC methods do not bootstrap
• the computational expense of estimating the value of a single state is independent of the number of states
  • this can be attractive when one requires the value of only one subset of states
  • one can generate many sample episodes starting from the states of interest
    • averaging returns from only these states ignoring all others